1. Einführung
2. Gravitation, Entropiekraft und Raumzeit
3. Entropiekonstante des kosmischen Universums
4. Dunkle Energie und Dunkle Materie
5. Beschleunigte Expansion des Universums
6. Grenzwerte im Mikrokosmos
7. Betrachtungen im übergreifenden Universum
8. Entropiekraft und Dunkle Materie in kosmischen Systemen
9. Quantenphysikalische Gravitations-, Entropie- und Energiefelder
10. Bosonen, Fermionen und das Gravitationsentropiefeld
11. Massen, Ladungen und Energien von Elementarteilchen
12. Quantenmechanische Vermittlung der vier Fundamentalkräfte
13. Entropiefeld und Kosmologisches Standardmodell
14. PDF Download / Tabellen A und B
7. Betrachtungen im übergreifenden Universum
Abgesehen von Schwarzen Löchern und sich extrem eng umkreisenden Doppelsternsystemen liegen die Markierungen im rechten Bildteil der nächstfolgenden Abbildung zwischen zwei im logarithmischen Maßstab parallelen Linien, welche der Funktion

durchaus folgen könnten. Die Anstiege a, im logarithmischen Zusammenhang die Parallelverschiebungen, liegen dann in einem Bereich zwischen 10-30 und 10-20 m5 kg-3.
Wenn man nun die Gleichung (27) als identisch mit Gleichung (8) ansieht, und wenn man annimmt, der Anstieg a sei der Quotient aus der Gravitationskonstanten ζ und der Entropiekonstanten ω, wären die beiden blauen Linien (siehe Abbildung) nichts anderes als ein Gleichgewichtszustand zwischen der Gravitations- und Entropiekraft wie im Kapitel über das Universum beschrieben.
Die gestrichelte blaue Linie in Abbildung 3 in Form von Gleichung (8) kommt der Entropiekonstante ω, so wie wir sie für unser Universum (ω ≈ 1018 kg2 m-2 s-2) diskutiert haben, nahe. Allerdings kann sie nicht das übergreifende Universum aus Mikro- und Makrokosmos repräsentieren. Selbst bei einer Verkleinerung von ω bis zur durchgezogenen blauen Linie (ω ≈ 1010 kg2 m-2 s-2) verblieben noch immer komplette kosmische Systeme deutlich oberhalb dieser gedachten Linie. Für Sonnensysteme und Galaxien wäre das zwar noch einigermaßen hinnehmbar. Es bedeutet aber trotzdem, dass dort und darüber hinaus in weiten Bereichen kosmischer Systeme die Entropiekräfte über die Gravitationskräfte dominieren würden und das wäre reiner Unsinn.
Bei der ω-9-Linie allerdings sähen sich nur die äußeren Bereiche von Galaxienhaufen, Galaxien und Sonnensystemen dem beginnenden Einfluss der Entropiekraft ausgesetzt. In den inneren Gebieten der Galaxien bzw. dem uns bekannten Teil unseres Sonnensystems fiele die Entropiekraft nicht ins Gewicht, da sie dort gemäß Gleichung (2) vollkommen vernachlässigbar wäre.
Die ω-9- hätte gegenüber der ω-18-Linie noch den weiteren Vorteil, dass sie sowohl direkt als auch indirekt (über die Planck-Marken der Wellenlänge / des Radius sowie der Energie / Masse) vermeintlich markante Anhaltspunkte im mikroskopischen Universum zu mindestens tangiert, was der ω-18-Graph ganz offensichtlich nicht so gut vermag. Die ω-9-Linie scheint irgendwie einen Zusammenhang mit dem Elektroschwachen Symmetriebruch (Sb), dem Wellenlängenbereich der Photonen (Ph) und dem Ende des Langwellenbereiches (d) herstellen zu wollen.
Aus den genannten Gründen wollen wir die Gleichgewichtsformel nach (8) mit einer Entropiekonstanten von vorerst 109 kg2 m-2 s-2 anwenden.
Abbildung 3: Mögliche übergreifende Zusammenhänge im logarithmisierten Energie (Masse)-Wellenlängen (Radius)-Diagramm

Um wirklich genau zu vergleichen (im logarithmisierten Diagramm liegt man schnell mal um Zehnerpotenzen daneben) und um präzise Berechnungen anstellen zu können, bedienen wir uns (weshalb wird weiter unten erläutert) dem exakten Wert einer Entropiekonstanten für das übergreifende Universum von ωυ = 5,31221·109 kg2 m-2 s-2.
Ohne weitere Begründung wenden wir einfach die Formel (8) gleichsam im gesamten Universum an. RGG wird im Mikrokosmos auf die reduzierte Comton-Wellenlänge λ von Elementarteilchen und Quanten, im Makrokosmos auf den Radius zu betrachtender Systeme, unabhängig von geformten Volumina (also beispielsweise ohne π-behaftete Faktoren) der zu betrachtenden Systeme, bezogen. Des Weiteren machen wir im Mikrokosmos, was die Entropiekraft betrifft (im Unterschied zum makroskopischen Maßstab), keinen Unterschied zwischen baryonischer Masse und Energiewerten. Ruhemasselose Teilchen wie Photonen gehen formelmäßig mit der ihrer Energie zuordenbaren (m = E/c2) Masse mS ein. Elementarteilchen und Quanten werden also quasi den kosmischen Systemen vollkommen gleich gestellt. Scheren wir sie einfach über einen Kamm und nennen sie „Systeme“. Mit der obigen Entropiekonstanten ergibt sich aus Gleichung (8) folgende Formulierung:

Wie man aus Abbildung 3 sofort entnehmen kann, werden die abnehmenden Radien R (Abstände) bei immer größer werdender Gravitation, was die Größe stabiler Systeme betrifft, durch den Schwarzschild-Radius begrenzt.
Nehmen wir nun an, dass die aus der Entropiekraft herrührende Beschleunigung die Raumzeit ebenso stark krümmen kann wie die gravitative Beschleunigung, muss es allein aus relativistischen Gründen jenseits der Dominanz der Entropiekraft ähnlich des Horizontes eines Schwarzen Loches ebenfalls eine solche Grenze geben. Wenn nun nach Einstein jegliche Beschleunigungskräfte Scheinkräfte sind und diese durch eine freie Bewegung einer Testmasse m1 im Beschleunigungsfeld wegtransformiert werden können, so muss das konsequenterweise auch für die durch die Entropiekräfte hervorgerufenen Beschleunigungen gelten. Da das Entropiepotential Beschleunigungen von innen nach außen anwachsen lässt und damit eine negative Energiefreisetzung nur bezüglich der im Systemzentrum befindlichen glatten Raumzeit stattfindet, wird durch die deshalb bedingte Integralumkehr das entropische Beschleunigungspotential ΦEntr nunmehr negativ.

Der negative Term aus Gleichung (29) muss sich nun nur noch mit dem positiven Bewegungspotential Φkin = v2 gebundener Systeme gS eliminieren,
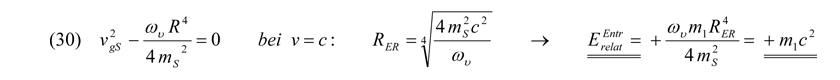
was umgestellt nach der relativistischen Grenze RER, die wir den Entropiekraft-Radius nennen wollen, eine neue, den Makro- mit dem Mikrokosmos verknüpfende, Gleichung ergibt. Im absoluten relativistischen Grenzfall gebundener Systeme entsprechen damit die entropischen positiven Energiebeträge genau dem Einsteinschen Masseäquivalent m·c2.
Die folgende Abbildung zeigt uns noch einmal die Zusammenhänge mit dem neuen Graphen des Entropiekraft-Radius:
Abbildung 4: Grenzwerte, Beziehungen und Lage von Systemen im Mikro- und Makrokosmos
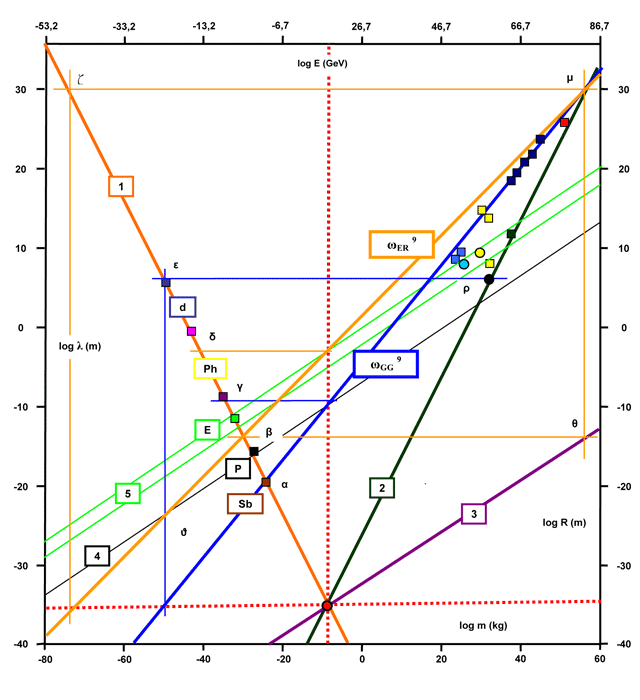
Nun wollen wir sowohl die Schnittpunkte auf der reduzierten Comton-Linie berechnen als auch einige interessante Zusammenhänge und Symmetrien mathematisch nachvollziehen. Denn wie auf dem ersten Blick scheint, so jedenfalls deutet es Abbildung 4 an, könnte das gesamte aus Mikro- und Makrokosmos bestehende Universum zu mindestens im logarithmischen Maßstab strengen geometrischen Regeln folgen. Ob dies wirklich der Fall ist bzw. ob es sich tatsächlich um irgendwelche Gesetzmäßigkeiten handeln könnte, soll die folgende Zusammenstellung auflösen. Die zu berechnenden und interpretierenden Punkte werden durch kleine griechische Buchstaben markiert, so wie man sie auch in Abbildung 4 wieder findet. Hier die umfassende rechnerische Zusammenstellung dazu:
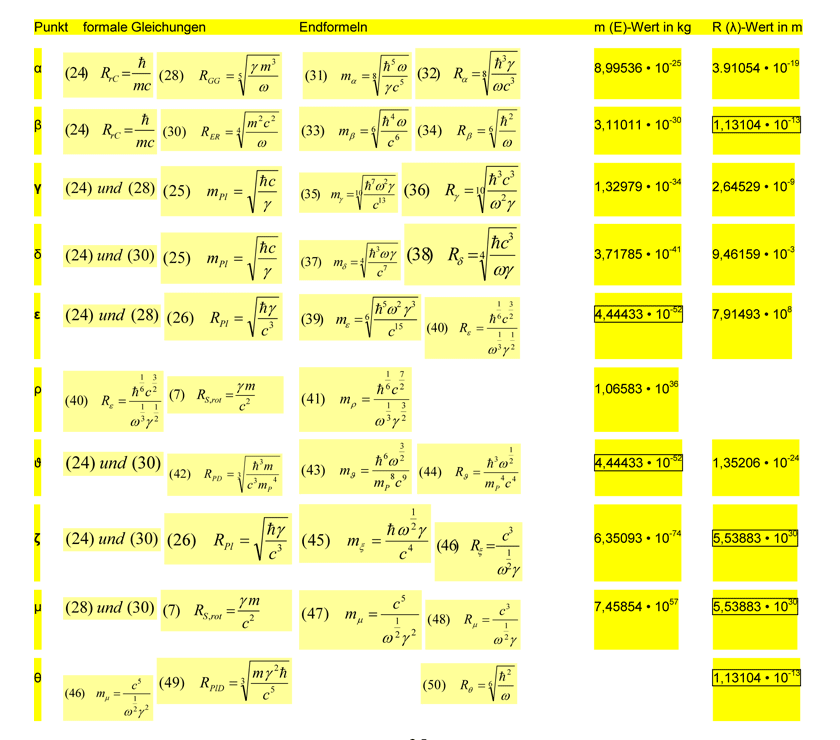
Die scheinbar ins Auge stechenden logarithmischen Symmetrieanteile in Abbildung 4 können jetzt auch mathematisch bestätigt werden. Wenn man als untere Basis die Planck-Länge nimmt, so grenzen die Punkte ζ und μ das hier beschreibbare übergreifende Universum durch die Logarithmen ihrer Masse- und Skalenwerte wie folgt ein:
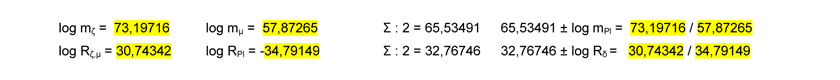
Es zeigt sich, dass die Achse der Planck-Masse mPl die Mittelachse des übergreifenden Universums darstellt, während der Graph des Entropiekraft-Radius RER diese Achse genau in ihrem Mittelpunkt bei Rδ schneidet. Die logarithmischen Abstände auf der Längenskala sind exakt halb so groß wie die auf der Massenskala bzw. anders ausgedrückt: Die logarithmischen Massenskalen jenseits der Planck-Masse entsprechen genau der Längenskala des übergreifenden Universums, was nichts anderes bedeutet, als dass der Mikrokosmos logarithmisch symmetrisch mit dem Makrokosmos verknüpft erscheint.
Eine andere Symmetrie liefern die gleichen Skalenwerte des Punktes θ auf dem Graphen der Planck-Dichte mit dem des Schnittpunktes der Entropiekraft-Linie mit der reduzierten Comton-Wellenlänge β.
Diese Symmetrien sind allerdings unabhängig von der Größe der Entropiekonstante ω. Verbunden mit den Formeln für den Gleichgewichts- und dem Entropiekraftradius sollte hier wohlmöglich nur ein allgemeiner geometrischer Zusammenhang nachgewiesen worden sein. Die Konstante ω legt also lediglich den genauen Rahmen des übergreifenden Universums fest. Und da dieses Universum nicht willkürlich sein sollte, muss die Entropiekonstante wie oben beschrieben an die makro- und mikroskopischen Gegebenheiten angepasst und beispielsweise wie folgt exakt beschrieben werden:
Die Entropiekonstante ω soll hier über den Schnittpunkt des Gleichgewichts-Radius mit der Planck-Länge und dem virtuellen Schnittpunkt der Protonendichte (mP: Protonenmasse) mit dem Entropiekraft-Radius normiert worden. Das heißt, die Punkte ϑ und ε sowie der Schnittpunkt des Gleichgewichtsgraphen mit dem der Planck-Länge sollen gleich große Massewerte aufweisen. Durch Gleichsetzen und Umstellen der Formeln (39) und (43) erhält man Gleichung (51). Natürlich muss sich dieser so normierte Wert einer Entropiekonstante für das übergreifende Universum im Weiteren erst noch bewähren.
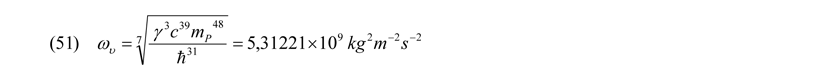
Außerdem sieht es so aus, als ob es unterhalb einer Linie ε – ρ im Makrokosmos keine dauerhaft gravitativ eigenständigen Systeme geben sollte, ebenso wie oberhalb dieser Linie im Mikrokosmos keine energetisch relevanten Elementarteilchen mehr existieren.
Zum Ende dieser Ausführungen werden die Symmetriebrüche und die Zwischenbereiche zusammengefasst (und zugegebenermaßen etwas überschäumend interpretiert), welche durch die Gleichgewichts- und Entropiekraft-Linie sowohl direkt als auch über die Planck-Werte indirekt auf dem reduzierten Comton-Graphen markiert werden. Dazu die folgende Aufstellung:
Tabelle 2: Quantenphysikalische Symmetriebrüche und Zwischenbereiche

>>> zum nächsten Kapitel (Entropiekraft und Dunkle Materie in kosmischen Systemen) >>>
