1. Einführung
2. Gravitation, Entropiekraft und Raumzeit
3. Entropiekonstante des kosmischen Universums
4. Dunkle Energie und Dunkle Materie
5. Beschleunigte Expansion des Universums
6. Grenzwerte im Mikrokosmos
7. Betrachtungen im übergreifenden Universum
8. Entropiekraft und Dunkle Materie in kosmischen Systemen
9. Quantenphysikalische Gravitations-, Entropie- und Energiefelder
10. Bosonen, Fermionen und das Gravitationsentropiefeld
11. Massen, Ladungen und Energien von Elementarteilchen
12. Quantenmechanische Vermittlung der vier Fundamentalkräfte
13. Entropiefeld und Kosmologisches Standardmodell
14. PDF Download / Tabellen A und B
3. Entropiekonstante des kosmischen Universums
Unter der Annahme, dass der galaktische Raum während der Zeit mittels drei Dimensionen expandiert, vereinfacht sich die Formel (2), nun angewandt auf das gesamte Universum U, wie folgt,
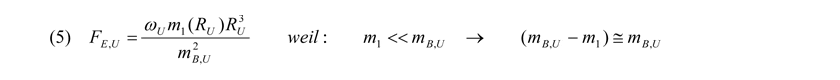
wobei RU der äußerste Radius an dem die Entropiekraft bestimmt werden soll und mB,U die gesamte baryonische Masse des Universums darstellt.
Mit Hilfe von Gleichung (4) kann man die Entropiekonstante ωU unseres Universums nur dann berechnen (angenommen die baryonische Masse des Universums bleibt während seiner gesamten letzten Entwicklungsphase im Schnitt konstant), wenn uns RU im Gleichgewicht von Gravitations- und Entropiekraft bekannt ist.
Dazu bedarf es eines weiteren Postulates, welches wegen nachfolgender Betrachtungen durchaus gerechtfertigt sein sollte.
Postulat 2: Der Wendepunkt des Gleichgewichtszustandes der Gravitations- und Entropiekraft deckt sich als Schwarzschildradius RS eines angenommen nicht rotierenden Schwarzen Loches mit dem Radius RU,GG unseres Universums an genau jenem Gleichgewichtswendepunkt.
Das heißt, dass unser Universum quasi eine Vergangenheit als expandierendes nicht rotierendes Schwarzes Loch hatte und ab dem Erreichen des Schwarzschildradius von der Entropiekraft beeinflusst wird. Eine weitere wichtige Aussage, welche sich aus dem Postulat ergibt, ist, dass genau am Wendepunkt des Kräftegleichgewichtes unseres Universums dessen Kritische Dichte erreicht worden war.
Dazu aber später, nachdem die Formeln für den Schwarzschildradius, auf zugegebenermaßen empirische Art und Weise, als Grenzwertbetrachtung hergeleitet worden sind. Folgende Überlegungen: Nach dem Virialsatz der Mechanik können Kraftwirkungen aus gravitativen Beschleunigungen aG dergestalt aufgehoben werden, dass ein entgegen gesetztes Kraftfeld gleichen Betrages provoziert wird, welches sich aus einer Drehbeschleunigung aD ergibt. Das sieht dann folgendermaßen aus,

wobei mZ die dominierende Gravitation ausübende zentrale Masse, vr die Rotationsgeschwindigkeit und R der Abstand vom Mittelpunkt der kugelförmig angenommenen zentralen Masse darstellen soll. Je näher sich also ein Objekt an die zentrale Masse heranbewegt, desto schneller müsste es rotieren, um nicht ins gravitative Zentrum fallen zu müssen. Dies kann allerdings nur bis maximal zur Lichtgeschwindigkeit c (2,99792458 · 108 ms-1) erfolgen, da diese eine fundamentale physikalische Konstante ist. Umgekehrt gedacht heißt das ebenso, dass alles, selbst Photonen, ab einem bestimmten Radius R einer Zentralmasse mZ, welche eine sehr große Masse in dem besagten Radius unterbringt, gefangen gehalten werden. Oder anders ausgedrückt: Ab einem bestimmten Radius einer genügend kompakten Masse wird von dieser alle Energie und Materie aufgesogen und jene demnach zu einem so genannten Schwarzen Loch. Gleichung (6a) nach R aufgelöst ergibt für vr gleich c den Schwarzschildradius eines rotierenden Schwarzen Loches.
Über die Gleichsetzung der Arbeit einer Testmasse im Gravitationsfeld mit deren kinetischer Energie gelangt man durch eine im Ergebnis ähnlich wie oben gelagerte Argumentation direkt zum Schwarzschildradius nicht rotierender Schwarzer Löcher,

sodass man, ähnlich der Herbeiziehung von Fluchtgeschwindigkeiten bezüglich dominierender gravitativer Massen, wegen der Konstanz der Lichtgeschwindigkeit zu diesen zwei Ergebnissen kommt:
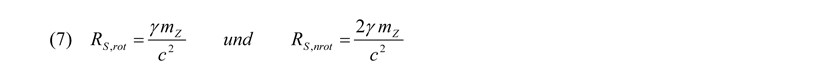
Nun kann man an die Berechnung der Entropiekonstanten ωU gehen, weil man, wie in den Gleichungen (4) aufgezeigt, die zweiten Ableitungen nach RZ gleich setzen und nach dem Radius RZ gleich RGG im Gleichgewichtszustand auflösen kann. Da nun mZ gleich mB ist, ergibt sich folgender formaler Zusammenhang:

Jetzt führt man gemäß Postulat 2 in RU,GG der Gleichung (8) den Schwarzschildradius RS,nrot aus Gleichung (7) ein und stellt nach der Entropiekonstanten ωU um. Bezogen auf unser Universums erhalten wir dann:

Um die Entropiekonstante allerdings konkret ausrechnen zu können, fehlt uns noch die Masse mB,U des Universums. Diese kann man mit Hilfe des Postulates 2 (Wendepunkt auf dem Schwarzschildradius) unter zur Hilfenahme der Friedmann-Gleichung der ART bezüglich der Kritischen Dichte des Universums ableiten. Demzufolge berechnet sich die Kritische Dichte ξkr nach:

Den aktuellsten Wert der Hubble-Konstante Ho aus den Auswertungen der WMAP-Mission, sowie die Größe der Gravitationskonstante γ mit ihren Einheiten, sind neben der Gleichung (10) angegeben. Nach oben genanntem Postulat 2 ist hier die Kritische Dichte nichts anderes als die Masse des Universums geteilt durch das Kugelvolumen, welches vom Schwarzschildradius bestimmt wird. Daraus folgt:

Fügt man nun die Formel für den Schwarzschildradius ein und löst die Gleichung (11) nach mB,U auf, erhalten wir die baryonische Masse des Universums:

Wenn man jetzt diese Masse wiederum in die Formel des Schwarzschildradius einsetzt, ergibt sich der Radius des Universums RU,GG im Gleichgewichtszustand, was nichts anderes als der Hubble-Radius RHo ist:

Nun fügt man nur noch den Wert aus Gleichung (12) in Gleichung (9) ein und erhält somit die Entropiekonstante ωU unseres Universums:
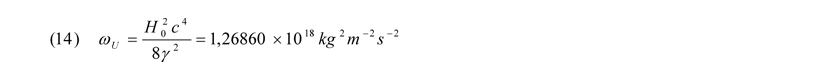
>>> zum nächsten Kapitel (Dunkle Energie und Dunkle Materie) >>>
