1. Einführung
2. Gravitation, Entropiekraft und Raumzeit
3. Entropiekonstante des kosmischen Universums
4. Dunkle Energie und Dunkle Materie
5. Beschleunigte Expansion des Universums
6. Grenzwerte im Mikrokosmos
7. Betrachtungen im übergreifenden Universum
8. Entropiekraft und Dunkle Materie in kosmischen Systemen
9. Quantenphysikalische Gravitations-, Entropie- und Energiefelder
10. Bosonen, Fermionen und das Gravitationsentropiefeld
11. Massen, Ladungen und Energien von Elementarteilchen
12. Quantenmechanische Vermittlung der vier Fundamentalkräfte
13. Entropiefeld und Kosmologisches Standardmodell
14. PDF Download / Tabellen A und B
9. Quantenphysikalische Gravitations-, Entropie- und Energiefelder
Konsistent mit den Gleichungen (31) bis (50) und den Daten der Tabelle B werden Wellenfunktionen quantenphyskalischer Systeme T nun mittels der alternierenden Gravitations- und Entropiefelder innerhalb der durch die Heisenbergschen Unschärfe gesetzten Potentialtöpfe folgender Längen Rλ beschrieben:

Da es nun einmal so ist, dass die potentielle Energie Epot eines derartigen quantenphysikalischen Systems T nur dann exakt und abschließend beschrieben werden kann, nachdem wegen der Endlichkeit und Konstanz der Lichtgeschwindigkeit c (die Information über die Energie verbreitet sich mit c) eine bestimmte Zeitspanne Δtλ als Funktion von Rλ abgelaufen ist, bekommen die entsprechenden Wellenfunktionen per se einen spezifisch relativistischen Charakter der Einsteinschen Theorie (SRT).

Dass die allgemeinen Gleichungen (69) und (70) nichts Weiteres darstellen als die quantenmechanische Variante des Gravitationsfeldes und wie sich unter Hinzuziehung der Entropiepotentiale daraus die vier fundamentalen Kräfte entwickeln wird im Weiteren noch ausführlich diskutiert werden.
Die allgemein-relativistische Wellenfunktion von Teilchenfeldern, bestehend u.a. aus der Arbeit F·R im Potentialtopf Rλ, nun jedoch mit den gemäß der Theorie eingeführten entropischen Anteilen, stellt sich jetzt wie folgt dar:
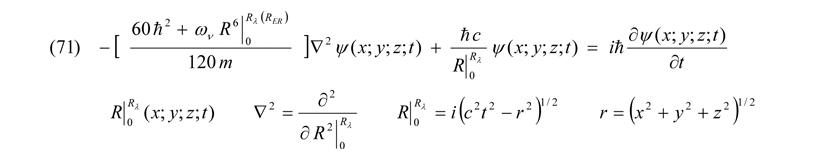
Der in Gleichung (71) in der eckigen Klammern auftauchende additive zweite Term ωR6/120m ergänzt nun den üblicherweise allein vor dem Hamilton-Operator und dem Input der Wellenfunktion stehenden Term der allgemeinen Formulierung für Spin-0-Teilchenfelder ħ2/2m. Die Symmetrie innerhalb des Potentialtopfes (R<Rλ) kann nun, je nach Größe der beteiligten Skalen und jeweiliger in der Schrödingergleichung unterschiedlicher nach den Raumkoordinaten und der Zeit realisierten Ableitungen, sowohl erhalten bleiben als auch mehr oder weniger stark gebrochen werden. Die Interpretation von Feldern für Teilchen mit einem Spin größer Null sowie für Teilchen mit einer Ruhemasse m0 sollte so möglich sein. Da mir leider die mathematischen Voraussetzungen fehlen, die Gleichung (71) bezüglich mikroskopischer Energiesysteme zu lösen, verwende ich im Folgenden einen grob vereinfachten Algorithmus, welcher im Resultat auch als Überblick in der Tabelle B zu ersehen ist:
1. Energiefelder virtueller Teilchen (T) entstehen durch Superponierung von Energie (E) und Masse (m) in oszillierenden Systemen bestehend aus identischen virtuellen Materie-Antimaterie-Paaren in Potentialtöpfen gemäß Gleichung (69):

2. Diese Superponierung wird erweitert um die Gravitations- und Entropiepotentiale (G bzw. E) aus Gleichung (71), als Mischzustände sowohl der Planck- (RPlanck) wie auch von Potentialtopf-Längen (Rλ):

3. Als Ergebnis dieser Betrachtungen sollen somit aus dem Vakuum heraus in den jeweiligen Potentialtöpfen ständig Energiefelder für zugehörige Elementarteilchen erzeugt werden, welche im nicht gestörten Zustand Funktionen stehender Wellen mit ganz spezifischen Schwingungsmustern und damit Energien und -zuständen entsprechen. Die Aufsummierungen bzw. Kombinationen der positiven und negativen Energieanteile ET,n aller Wellenfunktionen ψΣ,n in den betreffenden Potentialskalen Rλ,n im gesamten Universum ergeben gleich Null.
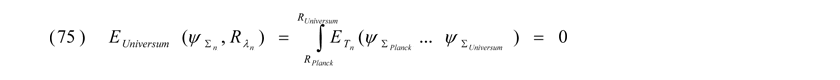
Diese Systeme bestehen wie schon gesagt aus oszillierenden Materie-/ Antimateriepaaren, welche über die o.g. Definitionen in den unscharfen Potentialtöpfen immerwährend aus dem Vakuum heraus gebildet und anhiliert werden können und damit als virtuell zu betrachten sind.
Bezüglich der Vakuum-Energiedichte nach Gleichung (75) des Gravitationspotentials für die kleinsten Skalen unseres Universums bedeutet dies einen Wert von:
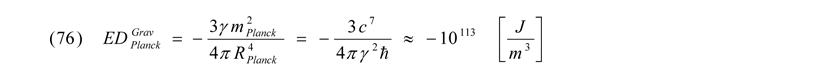
Für das dementsprechende Entropiepotential errechnet man unter Verwendung der Entropiekonstanten ωU des Universum nach (14) die untenstehende Energiedichte:

Bezogen auf Ausdehnung und Masse unseres Universums nach den Gleichungen (12) und (21) erhält man Energiedichten für das klassische Gravitations- und Entropiepotential folgender Größenordungen:

Betrachtet man hingegen RUniv als Potentialtopf Rλ wie in Gleichung (69) und ordnet dem Radius des Universum gemäß der Heisenbergschen Unschärferelation seine quantenphysikalische Masse zu (umgekehrt ergibt diese Transformation keinen Sinn, da man hier Rλ bedeutend kleiner als die Planck-Skala erhalten würde), berechnen sich nun diese Energiedichten:
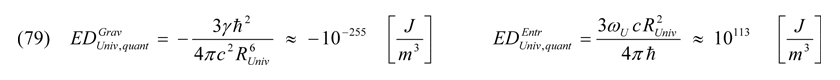
Was die Vakuum-Energiedichten auf den kleinsten und größten Skalen unseres Universums in quantenphysikalischer und globaler Hinsicht betrifft, ergeben sich hier durchaus konsistente Ergebnisse. Ebenso bezüglich (75) einer Gesamtenergiebilanz von Null. Die um zwei Zehnerpotenzen höhere Energiedichte des Entropiepotentials in Gleichung (78) bestätigt abermals die schon weiter oben gemachten Aussagen über die Ursache Dunkler Materie sowie der Dunklen Energie nebst ihrer antigravitativen Wirkung.
Durch die Aufsummierung von Gravitations- und Entropiekraftpotentialen können sich Gleichgewichts- und durch die Konstanz der Lichtgeschwindigkeit Grenzzustände innerhalb und außerhalb der jeweiligen Potentialtöpfe bilden.
Als Potentialgrößen sollen hier die ersten Ableitungen der Kräfte nach der Energie eines Materie- (Antimaterie)-teilchens dienen. Diese Beschleunigungsfelder (Potentialgradienten dφ(Rλ): im weiteren Potentiale bzw. Felder φ genannt) ergeben sich dann unter Berücksichtigung der Superpositionierungsbedingungen von (72), (73) bzw. (74) wie folgt für das Gravitationspotential
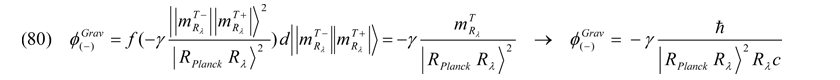
sowie für das Entropiepotential
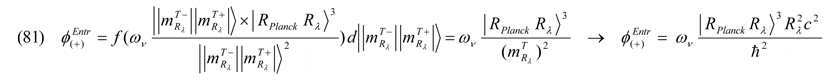
wobei, da immer φΣ = φGrav – φEntr gilt, es nun vier Möglichkeiten gibt, Potentialgrenzgrößen für ein und dieselbe Art virtueller Teilchen-Antiteilchen-Felder darzustellen:
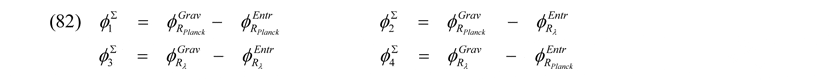
Des Weiteren ergeben sich aus Gleichung (82) für φΣ3, wenn man die 2. Ableitung nach Rλ bildet und diese gleich Null setzt, folgende Längen RGG für den Abstand im Potentialtopf, in denen das Potential im Feld einen Gradienten von Null annimmt:
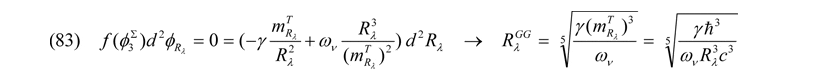
Zu beachten ist außerdem, dass es drei relativistische Grenzbedingungen gibt. Die erstere stellt bekanntermaßen das Planckteilchen mit der Masse mPlanck und den Abmaßen Rplanck als energiereichstes Quant dar. Alle weiteren quantenphysikalischen (gravitativ!) wirkenden Potentiale sind gemäß der ART nicht relativistisch. Neben dem Planckteilchen und den mit Gleichung (70) charakterisierten relativistischen Ansatz der Speziellen Relativitätstheorie (SRT) aus der Unschärferelation heraus, ergibt sich bei den Entropiepotentialen eine relativistische Grenzbedingung, aus welcher sich, wie noch zu diskutieren, ganz diffizile Eigenschaften der Elementarteilchen ableiten lassen können. Diese dritte relativistische Grenze RλER in gebundenen Systemen kommt zustande, wenn man Bewegungs- und Entropiepotentiale gemäß (29) und (30) gleich Null setzt. Abgesehen von der Planck-Energie hat man somit auf einer ganz anderen Ebene einen Zusammenhang der Mikrophysik mit der Allgemeinen Relativitätstheorie (ART) hergestellt:
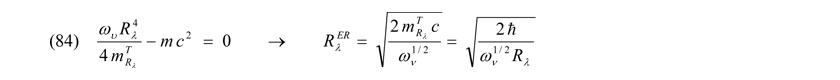
Mit diesen in Kapitel 9 gemachten Formulierungen (69) bis (84) und den dazu dargelegten Erläuterungen wurden die Betrachtungen des Kapitels 7. bestätigt, weitergeführt und konkretisiert. Insbesondere betrifft dies die dort gemachten Herleitungen der Gleichungen (31) bis (50), welche sich beim Durchlaufen von quantenphysikalischer Masse- bzw. Energiewerten innerhalb der Potentialtöpfe der Bedingung (69) hier ebenso ergeben würden. Davon kann man sich anhand von Tabelle B ein Bild machen. Die oben dargestellten vier Potentiale φΣ1 bis φΣ4 einzelner Teilchenfelder (Gleichung 82) und ihre Grenzen im Potential (Gleichungen 83 und 84) werden im Folgenden immer wieder herangezogen, um die Eigenschaften der Felder im Wechselspiel mit den dazugehörigen Elementarteilchen zu diskutieren.
>>> zum nächsten Kapitel (Bosonen, Fermionen und das Gravitationsentropiefeld) >>>
